Boundary Layer Parameters

Three main parameters (described below) that are used to characterize the size and shape of a boundary layer are the boundary layer thickness, the displacement thickness, and the momentum thickness. Ratios of these thicknesses describe the shape of the boundary layer.

There are other such thicknesses, but they are not as common.

Boundary Layer Thickness

  

Figure 3: Boundary Layer Thickness

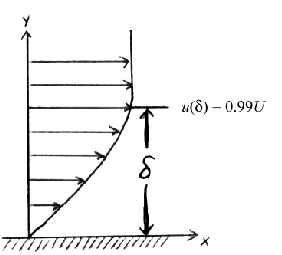
The boundary layer thickness, signified by $\delta$, is simply the thickness of the viscous boundary layer region. Because the main effect of viscosity is to slow the fluid near a wall, the edge of the viscous region is found at the point where the fluid velocity is essentially equal to the free-stream velocity.

In a boundary layer, the fluid asymptotically approaches the free-stream velocity as one moves away from the wall, so it never actually equals the free-stream velocity. Conventionally (and arbitrarily), we define the edge of the boundary layer to be the point at which the fluid velocity equals 99% of the free-stream velocity:

$$u\vert _{y=\delta} \equiv 0.99 U$$

Because the boundary layer thickness is defined in terms of the velocity distribution, it is sometimes called the velocity thickness or the velocity boundary layer thickness. Figure 3 illustrates the boundary layer thickness.

There are no general equations for boundary layer thickness. Specific equations exist for certain types of boundary layer. For a Blasius (flat-plate, incompressible, laminar) boundary layer, the boundary layer thickness is given by

$$\frac\delta x=\frac{4.910}{\sqrt{Re_x}}$$

where $x$ is the distance from the leading edge of the plate (Emanuel, 230).

Displacement Thickness

The displacement thickness, symbolized by $\delta^*$, is the distance a streamline just outside the boundary layer is displaced away from the wall compared to the inviscid solution. Another way to describe it is the distance the wall would have to be displaced to yield the same solution for flow outside the boundary layer as the boundary layer equations yield.

  

Figure 4: Displacement Thickness

Still another way to describe displacement thickness is in Figure 4. The displacement thickness is the distance that, when multiplied by the free-stream velocity, equals the integral of velocity defect, $U-u$, across the boundary layer. That is,

$$U\delta^* = \int_0^\infty(U-u)\,dy$$

Solving for $\delta^*$,

$$\delta^* \equiv \int_0^\infty\left(1-\frac uU\right)\,dy$$ (1)

The displacement thickness is important in iterative boundary layer solutions. After employing the boundary layer equations to calculate the displacement thickness along the wall, a virtual wall is created by displacing the wall outward by the displacement thickness. A new inviscid solution is computed using this virtual wall. This yields slightly different free-stream conditions than the initial calculation. The boundary layer solution is then recalculated, using the new free-stream conditions, for the real wall. The process is repeated until the displacement thickness stops moving with each iteration.

Momentum Thickness

The momentum thickness, symbolized by $\theta$, is the distance that, when multiplied by the square of the free-stream velocity, equals the integral of the momentum defect, $\rho u(U-u)$, across the boundary layer. That is,

$$\rho U^2\theta = \int_0^\infty\rho u(U-u)\,dy$$

Solving for $\theta$,

$$\theta \equiv \int_0^\infty\frac uU\left(1-\frac uU\right)\,dy$$ (2)

The momentum thickness is somewhat harder to visualize than the displacement thickness. One can visualize it using Figure 4, except that specific momentum flux distribution $u(y)^2$ replaces the velocity distribution $u(y)$.

The momentum thickness is useful in determining the skin friction drag on a surface. The total skin friction drag per unit depth on the surface is given simply by $\rho U^2 \theta$, evaluated at the trailing edge.