

Next: Transformation from Hodograph to
Up: Mathematical Description of the
Previous: General Hodograph Equation
To evaluate M, we assume a perfect gas. We define a parameter
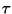 as:
as:
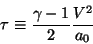 |
(15) |
Using the perfect gas relationship
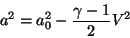 |
(16) |
we get 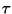 in terms of M:
in terms of M:
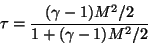 |
(17) |
The parameter 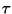 is somewhat like the characteristic Mach number;
it varies from zero at M=0 to one at
is somewhat like the characteristic Mach number;
it varies from zero at M=0 to one at 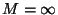 .
At Mach one,
.
At Mach one,
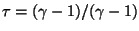 .
This value is written henceforth as
.
This value is written henceforth as
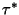 .
.
Solving Equation 17 for M2 gives
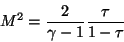 |
(18) |
And from Equation 15 we get
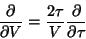 |
(19) |
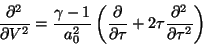 |
(20) |
Using Equations 18-20,
Equation 14 transforms to:
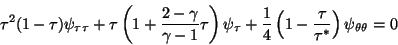 |
(21) |


Next: Transformation from Hodograph to
Up: Mathematical Description of the
Previous: General Hodograph Equation
Carl Banks
1999-05-14
![]() as:
as: