Trim

Trim is generally defined a condition in which none of the state variables change with time (that is, all of the state variable rates are zero). This does not, however, preclude accelerating conditions; the velocities must remain fixed in body axes, but will change direction in an inertial reference frame if the helicopter rotates. Trim conditions include straight and level flight, steady turns, and spins.

Determining the trim condition is an iterative process, as exact closed form solutions are not possible. The four helicopter controls, the collective, the longitudinal and lateral cyclic, and the tail-rotor cyclic, are adjusted along with some of the state variables until the state variable rates ($\dot u$, $\dot v$, etc.) go to zero. Because there are 12 variables to adjust (eight state variables and four control variables), while there are only eight state variable rates to zero, it follows that some of the state variables are determined from the prescribed trim condition rather than adjusted at each iteration.

For the calculations in this report, we prescribe a particular airspeed and horizontal, nonturning flight. The angular velocities ($p$, $q$, $r$) are zero. At a particular airspeed, the helicopter will trim to a particular orientation, but we do not know this orientation beforehand. Therefore, during the iteration, we will adjust Euler angles $\Phi$ and $\Theta$. Given the current guesses for $\Phi$ and $\Theta$, the velocity components are given by [from Padfield, 277]:
$$\begin{align*}u &= V\cos\Theta \\ v &= V\sin\Theta\sin\Phi \\ w &= V\sin\Theta\cos\Phi \end{align*}$$
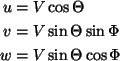
Now, looking at Equations 7 and 8, $\dot\Phi$and $\dot\Theta$ are zero because $p$, $q$, and $r$ are zero. This leaves $\dot u$, $\dot v$, $\dot w$, $\dot p$, $\dot q$, and $\dot r$to be zeroed.

There are six unknown variables ($\theta_0$, $\theta_{1s}$, $\theta_{1c}$, $\theta_{0T}$, $\Phi$, and $\Theta$), and six variables to zero. Solving this problem is the same as solving a system of nonlinear equations. I used Broyden's secant method to do this [see Dennis and Schnabel], which is an secant interpolation method for multivariable problems.